---

ニジボックスの案件事例をご紹介！

---

ABテストにおいて、AのデータとBのデータに甲乙つけがたい結果が出ることがしばしばあります。しかしWebマーケティングでは、AとBのデータの差に違いがあるのかを判断することは重要です。

そこで、本記事ではABテストの判定に関して、カイ二乗検定や統計学を用いた方法について詳しく解説していきます。

ABテストとは

ABテストはWebマーケティングにおいて、AパターンとBパターンを比較してどちらが効果的かをテストする手法です。

例えば、広告クリエイティブにおいてコーラを飲んでいる人物を見せるか、キンキンに冷えたコーラにフォーカスするか、2パターンのクリエイティブを出して検証できます。
以前は感覚的な判断が主でしたが、データを取得できるようになったことで、より厳密な結果を見つけられるようになりました。

また、個人でも無料のツールを使ってWebサイトデザインのABテストができます。
GoogleやFacebookもABテストを積極的に取り入れており、有名な例としてオバマ大統領の選挙ランディングページにおけるABテストが挙げられます。

ABテストについては下記の記事で詳しく解説しているので、ぜひ併せてご覧ください。

ABテストを行う必要性

Webマーケティングにおいて、ABテストは個人でも手軽に行うことができ、頻繁に使われる手法です。
ABテストを適切に行うことで、Webサイトやアプリの新規顧客開拓や売り上げの向上につなげられます。

ABテストを行うことは効果的な改善案の発見、ユーザーエクスペリエンスの向上、コストの削減やデータ主導の改善など多くのメリットがあります。
Webサイトやアプリの改善に取り組む上で、ABテストは有用な手法の1つと言えます。

ABテストを行う際の注意点

ABテストを行う際の注意点として、母集団がランダムサンプリングされているかどうかを確認することが必要です。
自動的にユーザーがランダムに振り分けられるABテストツールでも、手動でサンプルを振り分けた場合には、作為的な振り分けになってしまう可能性があります。

また、テストパターンを細かくしすぎると有意差が出るまで時間がかかったり、有意差が出なくなったりすることがあります。
したがって、サンプル数が多ければ多いほど有意差が出やすくなることを考慮し、テストパターンを適切に設計することが必要です。

ABテストにおけるカイ二乗検定

ABテストでは、カイ二乗検定によってテスト結果の有意差を測定します。

カイ二乗検定は、「分布に差が生じているか否かを測定する」という検定方法です。
例えば、メール件名のABテストを実施した場合、送信したメールのクリック率に有意差があるかどうかを調べる場合、カイ二乗検定を使って調査できます。

期待値と実測値の差を求め、差の二乗を期待値で割って足し合わせます。式は以下のとおりです。

得られた結果をカイ二乗値といい、カイ二乗分布と照らし合わせることで何％の確率で起こりうる値なのかを調べられます。

また、カイ二乗分布には自由度という指標が必要です。自由度は行数と列数から求めることができ、式は以下のとおりです。

ABテストから得られたデータが偶然かどうか、ABテストの信頼性が高いかどうかを、一般的には、5％有意もしくは1％有意を用いて判定します。

ABテストの有意差については下記の記事で紹介しているので、ぜひ併せてご覧ください。

ABテストで統計学を用いること

次に、ABテストで統計学を用いることについて解説していきます。
統計学はサンプルから得られたデータを使って、母集団の性質を推測する学問です。

ABテストでは単純にデータを比較するだけでなく、結果が偶然のものではないことを確認する必要があります。なぜなら、誤った結果に基づいて判断するとサイトの改善につながらなかったり、逆に悪化させてしまったりする可能性があるからです。

ABテストにおいてより正確な検証を行うためには、統計学的な手法を使用して、十分なサンプルサイズを確保する必要があります。

①標準偏差と区間推定

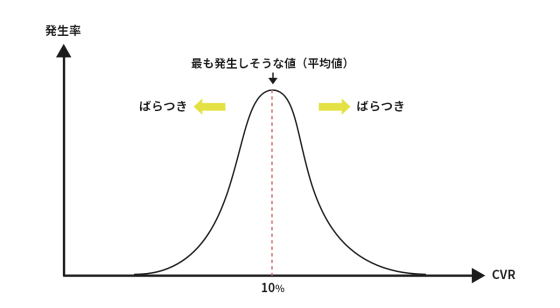
統計解析を考慮する場合、コンバージョンレート（以下、CVRと表記します）がキーの指標になってきます。
CVRを正しく解釈するには、「不確かさ」を把握する必要があり、統計学でいう「標準偏差」を示すことになります。
また、CVRの「不確かさ」を推定する方法として「区間推定」が挙げられます。

標準偏差と区間推定について解説します。

標準偏差とは何か

「標準偏差」は、各データが標準的に平均値からどれだけずれているかを示す数値です。
「偏差」は中心からのズレを表します。

「平均値」だけではデータのバラつきがわからないため、「標準偏差」を用いて平均値に対しての数値のバラつき度合いを把握できます。

例えば、CVRが10％で標準偏差が5％の場合、「CVRから±5％程度のズレがある可能性がある」という解釈になります。
標準偏差が大きいほどデータのバラつきが大きくなるため、統計解析において標準偏差は重要な指標となります。

区間推定とは何か

区間推定とは、平均値からのズレが標準偏差の範囲内に収まる確率を推定する方法です。
統計学上の「不確かさ」を持つCVRのバラつきが、範囲内に収まる確率を示します。

CVRの真の値（母数）を幅を持たせて推定する方法で、この±○○％の範囲を「信頼区間」と呼びます。
例）CVR：A％、標準偏差：B％の場合→±B％に収まる確率はC％

「不確かさ」は、分かっているようでも理解が難しい概念です。しかし、統計学の考え方を理解することで、CVRの値を正しく解釈することができます。

②CVR（コンバージョンレート）

CVRは、サイト訪問者数に対する成約の割合を示す指標です。
CVRを計算する際には、CV数（成約数）をどの数値で割るかが重要です。
PV（ページビュー）は1人のユーザーが複数回閲覧しても、閲覧回数をカウントしてしまうため、UU（ユニークユーザー）を使用する方が正確な判断ができます。

CVRには誤差があり、UU数やCV数の大小によって信頼性が変わってしまいます。
したがって、データを正しく解釈するためには、CVRの計算方法やデータの不確かさについて理解しておくことが重要です。

また、CVRの数値自体にも注意が必要です。
例えば、CVRが10％と90％であるとします。その場合、90%の成果率が高いことは分かりやすいです。

では、CVRが50％の場合はどう考えればよいのでしょう。
50％とは、可能性が半々ということなので、CVRが50％に近づけば近づくほど、不確かさが大きくなっていきます。
さらに、UU数が少ない場合には、不確かさが増すためCVRの解釈には、UU数とCVR数値の双方が関係していることを留意しておく必要があります。

CVRについては下記の記事で解説しているので、ぜひ併せてご覧ください。

③確率密度

次に、確率密度について解説していきます。

確率密度は①で解説した標準偏差や平均値、正規分布グラフから求めることができます。
統計学における基本的な知識の1つでもあるため、覚えておくと良いでしょう。

どうやって確率密度を求めるのか

標準偏差はデータのバラつきを表し、一般的に「平均値からどの程度離れているか」という指標として使われます。
標準偏差を使うことで、「平均値±1標準偏差」「平均値±2標準偏差」「平均値±3標準偏差」の範囲内にデータが収まる確率を求めることができます。

一方で、確率密度は指定した確率範囲のグラフから面積を求めることで算出できます。
確率密度はExcelのNORMDIST関数を使うことで、グラフから面積を計算することができます。

正規分布について

正規分布は左右対称の山のようなグラフで表されます。
グラフの形は標準偏差によって決まります。確率密度の概念を理解することで、グラフから得られたCVRの数値を正しく解釈することができます。

正規分布の中心にある平均値は、データ全体の中央点を表しています。
また、中央値はデータを小さい順に並べたときの中央の値を表します。中央値と平均値が一致していることは、分布が左右対称であるといえるでしょう。

CVRの数値を正しく解釈するためには、正規分布の概念を理解し確率密度の概念を用いて分布を読み解く必要があります。

検定の基本的な流れについて解説

ABテストでよく用いられるカイ二乗検定の説明に入る前に、検定とは何かについて解説します。

検定とは、主張したい仮説（対立仮説）とは異なる仮説（帰無仮説)）がまれにしか起こらないことを前提として、自分の主張が正しいということを示す統計学の手法です。

以下で、基本的な流れを見ていきましょう。

自分の主張する仮説とそうではない仮説

検定では帰無仮説と対立仮説の2つの仮説を設定し、帰無仮説が成り立つときに観測されたデータがどの程度珍しいかを評価します。

ABテストの場合、帰無仮説は「オリジナルと改善パターンのCVRに差がない」ことになります。
一方で、対立仮説は「オリジナルより改善パターンのCVRのほうが高い」という結果になります。

帰無仮説がまれにしか起こらないことを示すことで、オリジナルより改善パターンのほうがCVRが高いだろうということがいえるようになります。
検定は帰無仮説が成り立つときに、観測されたデータがどの程度珍しいかを評価するため、統計的な有意性を評価する手法として用いられます。

帰無仮説をもとに、その棄却領域が分かる

帰無仮説は有意水準（5%）を用いて棄却されるかどうかを判断し、標本平均が領域内に入ることは、主張される仮説がまれであることを意味します。

ここで、有意水準によって定められた領域を棄却域と呼びます。
棄却域に入った場合、帰無仮説が間違っている可能性があり、帰無仮説は棄却され対立仮説が採択されることになります。

このように、検定は帰無仮説を棄却することで、対立仮説が正しいことを示します。

平均値が棄却域に入るのかどうか調べる

そして、平均値が棄却域に入るのかどうか調べましょう。

まず、有意水準を決定しそれに基づいて棄却域を設定します。
次に、実際にデータを収集し標本平均を計算します。その値が棄却域に入っている場合、帰無仮説を棄却し対立仮説が正しいことが分かります。

ただし、標本平均が棄却域に入っていない場合、対立仮説が正しいとはいえません。
また、棄却域には片側検定と両側検定があります。
ABテストはオリジナルより改善パターンのCVRが高いことを主張するため、片側検定の右側を棄却域とするイメージを持っておくことが重要です。

カイ二乗検定の手順

最後に、カイ二乗検定の手順について解説していきます。
カイ二乗検定の手順は具体的には以下のようになっており、それぞれ順を追って解説します。

• 十分なデータを用意する
• 集計結果をまとめる
• 期待度数を算出する
• 偶然率を算出する
• 有意水準を比べる

カイ二乗検定は分類されたデータを比較する際に用いられ、実測値と期待値の差が大きくなるほど、帰無仮説を棄却することができます。

Step1 :十分なデータを用意する

統計学やデータ分析において、データの量が少なかったり偏りがあったりすると、結論で致命的な欠陥が生じる恐れがあります。

例えば、ABテストでページの遷移率を見るときに、元ページへのアクセス数が100の段階では「Aパターンの遷移率＝50％、Bパターンの遷移率＝10％」だったとしましょう。
しかし、アクセス数が10000に到達するころには、「Aパターンの遷移率＝5％、Bパターンの遷移率＝15％」のように逆転することもあります。

データの量が少ない状態で判定すると、偶然発生した一時的な結果を結論としてしまう可能性もあるため、十分なデータで判定することが必要です。

Step2 : 集計結果をまとめる

偏りのないデータが集められたら、次にクロス集計表などを用いてデータの集計を行います。
データを整理してまとめることによって、値のバラつきをふかん視することができ、より効果的なデータ分析を行うことが可能になります。

Step3 : 期待度数を算出する

次に、データから期待度数を求めていきます。
期待度数は「データにXという関係性がなかったらこの値になるだろう」という数値のことです。

期待度数を算出したら、データ実測値を先述したカイ二乗検定の式に入れて、カイ二乗値を求めます。

Step4 : 偶然率を算出する

そして、求めたカイ二乗値から変換公式を使い、p値（偶然率や検定推定量ともいう）を算出します。
p値は帰無仮説が正しい場合に、実測値以上の極端なサンプルがとれる確率のことを指しています。
p値が高ければ高いほど、帰無仮説は正しいといえます。

Step5 : 有意水準を比べる

有意水準は帰無仮説が間違っているといえる基準のことで、基本的には0.05の値を取ります。
そして、p値と比べて大きいかどうかを調べます。
仮に有意水準のほうが小さい場合、帰無仮説が正しく影響はないと判断できます。

一方で、有意水準のほうが大きく帰無仮説が棄却される場合、相反する対立仮説が正しいということになります。

まとめ

本記事は、ABテストを統計学やカイ二乗検定により判断する方法について解説してきました。
Webマーケティングにおいて重要とされているABテストは、統計学や検定を取り入れることでより効果的に検証することが可能です。

下記資料ではニジボックスがクライアント課題に伴走する中で磨き上げてきたユーザー視点を重視したUXデザインのプロセスや、ご支援事例の一部を紹介しています。
ご興味を持たれた方はぜひ、下記ダウンロードリンクよりご参照ください！